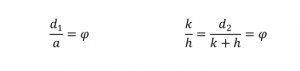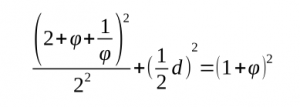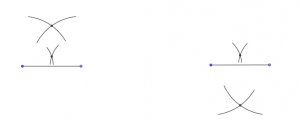Mozaika Penrose’a jako mozaika nieokresowa
Autor: Antonina Arkit
Przedstawimy aplet dynamiczny umożliwiający tworzenie mozaiki Penrose’a. W aplecie tym dostępne są elementy tej mozaiki, które można układać w dowolnych konfiguracjach.
Mozaika to wypełnienie powierzchni powtarzającymi się elementami bez pozostawiania pustych przestrzeni i nakładania się elementów na siebie, tworząc jakąś całość.
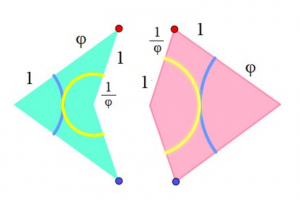
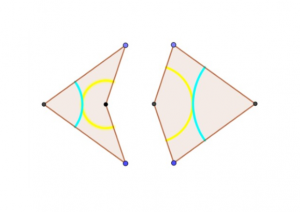
Mozaiki okresowe to takie, w których powtarza się jeden określony motyw, np. proste, kwadratowe kafelki. Mozaiki nieokresowe nie mają takiego motywu. Przykładem mozaiki nieokresowej jest mozaika Penrose’a złożona z dwóch elementów, które nazwę tu strzałką i latawcem:
Elementy te ściśle związane są ze złotą liczbą i tzw. złotą proporcją.
Złota proporcja to podział odcinka na dwie części w taki sposób, aby stosunek części dłuższej do krótszej wynosił tyle, ile stosunek całego odcinka do części dłuższej. Stosunek ten wynosi w przybliżeniu 1,618 i jest oznaczany grecką literą φ.
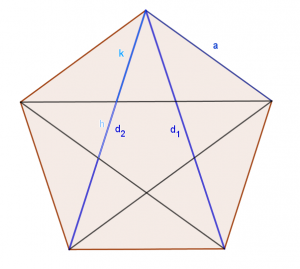
Pojawia się on w wielu miejscach. Dokładnie tyle wynosi stosunek przekątnych i boków pięciokąta foremnego:
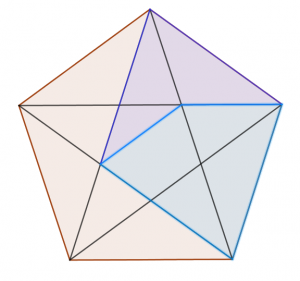
Obecność złotej liczby w mozaice Penrose’a widoczna jest w stosunku pola latawca do pola strzałki. Elementy te można wpisać w pięciokąt foremny:
Z tego wiemy, że proporcje w pięciokącie nakładają się na dane figury.
Ta liczba zawiera się również w bokach figur, co można zobaczyć na pierwszym rysunku (boki strzałki i latawca mają długości 1+ φ, 1+ φ, 1+ 1/φ, 1+ 1/φ).
Proporcję tę stosuje się w sztuce, np. w fotografii czy architekturze. Złoty podział w fotografii to zasada kompozycji, w której obszar dzieli się na 9 części według tej proporcji. W architekturze zaś można zobaczyć tę proporcję w różnych budowlach, jak w Wielkim Meczecie w Kairuan czy, jak się uznaje, w greckim Partenonie.
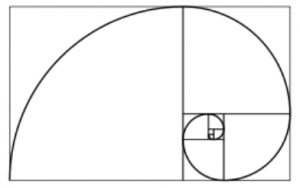
Występuje w ciągu Fibonacciego (0, 1, 1, 2, 3, 5, 8, 13, 21…), im wyższe liczby, tym stosunek dwóch kolejnych wyrazów tego ciągu bardziej zbliża się do złotej proporcji. Ciąg Fibonacciego można przedstawić w postaci spirali, w której podane wyrazy są długościami boków kwadratów:
Pod tą postacią pojawia się w przyrodzie:
w muszlach:
ramionach galaktyk:
lub płatkach kwiatów:
Aby skonstruować elementy mozaiki, potrzebujemy znać długość odcinka, który jest krótszą przekątną rombu powstałego ze strzałki i latawca.
Mamy dane długości boków oraz dłuższą przekątną (można zauważyć, że łuki nakładają się na siebie, stąd wystarczy dodać długości ich promieni). Możemy z tego skorzystać, aby obliczyć długość drugiej przekątnej (d=3,07):
Konstrukcja elementów mozaiki
-
Rysujemy odcinek o długości 3,07:
-
Zakreślamy z końców odcinka łuki z jednej strony odcinka o promieniu równym długości boku rombu, czyli 2,618:
-
Zakreślamy z końców odcinka łuki o długości 1,618:
-
W strzałce po tej samej stronie, gdzie był zakreślony bok rombu;
-
W latawcu po przeciwnej stronie od zakreślonego boku rombu;
-
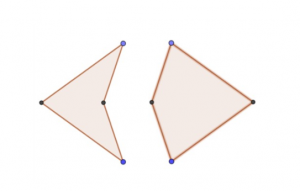
Łączymy cztery punkty, otrzymując oba czworokąty:
Możemy również wewnątrz figur narysować łuki o promieniu 1,618, 1 i 0,618:
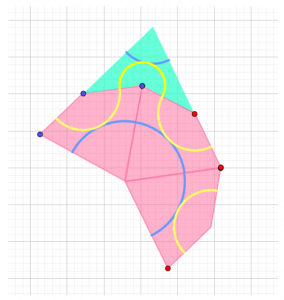
Na podstawie przedstawionej konstrukcji w GeoGebrze stworzyłam dwa narzędzia do wstawiania tych elementów i tworzenia mozaiki Penrose’a. W celu dodania kolejnej strzałki klikamy ikonkę trójkąta, w celu dodania latawca klikamy ikonkę rombu.
Efekt można zobaczyć poniżej (aby przesunąć figurę, używamy niebieskiego punktu, aby obrócić ją, używamy punktu czerwonego):