Autor: Aleksandra Arkit
Tangram to popularna łamigłówka znana w Chinach od ok. 3000 lat. Dzięki swojej specyfice potrafi przyciągać uwagę ludzi o różnym wykształceniu i zainteresowaniach. Dla matematyków stanowi niewyczerpane źródło zależności geometrycznych. Dla nauczycieli jest ciekawym środkiem dydaktycznym.
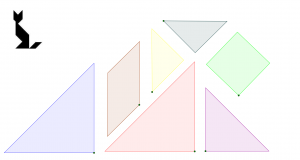
Tangram to kwadrat, który składa się z 7 części (tan): 2 duże trójkąty, 1 średni trójkąt, 2 małe trójkąty, 1 kwadrat, 1 równoległobok.
Celem tej gry jest ułożenie większego obrazka (figury) według przygotowanego wzorca (najczęściej narysowanych konturów tego obrazka) lub własnej wyobraźni.
Gra polega na ułożeniu wszystkich części, tak aby poszczególne elementy leżały obok siebie, ale nie mogą na siebie nachodzić. Tany można obracać na drugą stronę.
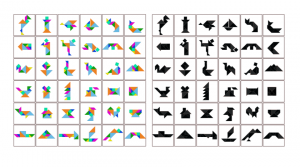
Za pomocą tangramu można ułożyć tysiące obrazków sylwetek ludzi i zwierząt, przedmiotów, figur geometrycznych.
Pomiędzy częściami tangramu istnieje mnóstwo zależności geometrycznych:
- pole dużego trójkąta jest dwa razy większe od pola trójkąta średniego,
- średni trójkąt, kwadrat i równoległobok mają takie same pole,
- pole średniego trójkąta jest dwa razy większe od pola trójkąta małego,
- kwadrat ma cztery kąty proste,
- równoległobok ma dwa kąty ostre po 45° oraz dwa kąty rozwarte po 135°,
- wszystkie trójkąty są równoramienne i prostokątne, a więc każdy ma jeden kąt prosty i dwa kąty po 45°,
- wszystkie trójkąty są podobne,
- przyprostokątna trójkąta średniego ma taką samą długość jak przeciwprostokątna trójkąta małego, przekątna kwadratu i jeden z boków równoległoboku,
- przyprostokątna trójkąta małego ma taką samą długość, jak bok kwadratu i drugi bok równoległoboku,
- kąt rozwarty równoległoboku i kąt ostry dowolnego z trójkątów są kątami przyległymi.
Poszukiwanie i sprawdzanie własności wielokątów może stanowić ciekawą, warsztatową lekcję powtórzeniową. Można również uwzględnić obliczanie obwodów figur. Warto zachęcić uczniów do wykonania odpowiednich pomiarów. W tym celu każdy uczeń powinien pracować ze swoim tangramem.
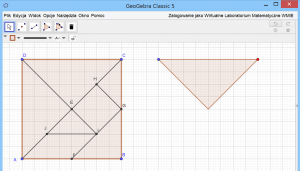
Jeżeli nie mamy odpowiedniej liczby układanek dla uczniów, to możemy wykonać ćwiczenie – powtarzając wiadomości o wielokątach i odcinkach w wielokątach – w wyniku którego każdy uczeń stworzy swój własny tangram. Ćwiczenie to polega na podaniu serii poleceń do wykonania na arkuszu kartonowym:
- narysuj kwadrat ABCD o boku równym 8 cm
- narysuj przekątną kwadratu AC
- zaznacz środek odcinka AC – punkt E
- narysuj odcinek łączący wierzchołek kwadratu D ze środkiem przekątnej kwadratu AC
- połącz odcinkiem środek boku AB (punkt F) oraz środek boku BC (punkt G)
- narysuj odcinek łączący środek boku BC ze środkiem połowy przekątnej kwadratu EC
- narysuj odcinek łączący środek odcinka FG ze środkiem przekątnej kwadratu AC
- połącz środek odcinka FG ze środkiem połowy przekątnej kwadratu AE.
Po otrzymaniu rysunku należy kwadrat wyciąć i poprzecinać wzdłuż narysowanych linii. Układanka gotowa, a satysfakcja gwarantowana.
Po zbadaniu własności figur i utworzeniu figury wg wzorca uczeń może wkleić efekt swojej pracy do zeszytu.
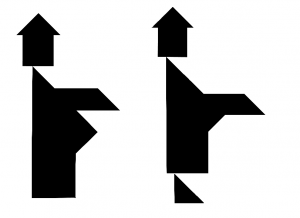
Aby zwiększyć zainteresowanie uczniów warto im zaprezentować paradoksy związane z tangramem: są to figury, które wydają się identyczne, a jednak różnią się i są ułożone w inny sposób. Warto podkreślić, że w rzeczywistości pole powierzchni obu figur jest takie samo. Skąd więc te różnice? Super wyzwanie dla młodocianych detektywów.
- paradoks wędrowca
- paradoks zbitego wazonu
Tangram pozwala również zilustrować twierdzenie Pitagorasa, aczkolwiek tylko dla trójkąta równoramiennego. Trzeba wykorzystać dwie – czasami trzy – układanki.
Ciekawostka i kolejne wyzwanie do sprawdzenia: W 1942 roku dwaj chińscy matematycy: Fu Tsiang Wang i Chuan-Chih Hsiung wykazali, że z elementów tangramu można skonstruować tylko 13 figur wypukłych. Rezultat swoich doświadczeń opublikowali w 49. tomie American Mathematical Monthly.
Kolejną propozycją do wykorzystania tangramu na lekcji jest samodzielne tworzenie tangramu w GeoGebrze. Więcej…








Chętnie poczytam coś jeszcze w tym temacie.
Natychmiast damy znać …