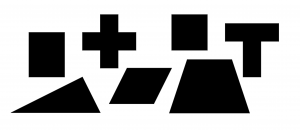Jakiś czas temu zaproponowaliśmy wykorzystanie Tangramu – popularnej łamigłówki znanej w Chinach od ok. 3000 lat – jako środka dydaktycznego na lekcjach matematyki.
Tym razem chcemy zachęcić do zabawy z układanką Samuela Loyda – amerykańskiego wynalazcy gier i wybitnego specjalisty od zagadek. Sam Loyd dokonał podziału kwadratu na pięć części:
z których można zbudować – układając poszczególne elementy tak, aby leżały obok siebie – prostokąt, pięciokąt, trapez równoramienny, krzyż grecki, równoległobok, kształt litery T:
Badanie własności geometrycznych poszczególnych części układanki proponujemy do wykorzystania na warsztatowej lekcji powtórzeniowej. Polecamy również uwzględnienie obliczania pól i obwodów figur. Warto zachęcić uczniów do wykonania odpowiednich pomiarów. Dobrze byłoby, gdyby każdy uczeń mógł pracować ze swoją układanką.
W tym celu możemy wykonać ćwiczenie – powtarzając wiadomości o wielokątach i odcinkach w wielokątach – w wyniku którego każdy uczeń stworzy swoją własną układankę. Ćwiczenie to polega na podaniu serii poleceń do wykonania na arkuszu kartonowym:
- narysuj kwadrat o boku równym 21 cm
- w każdym narożniku narysuj kwadrat o boku równym 7 cm – powstanie krzyż grecki
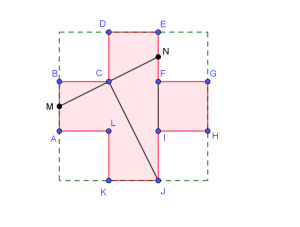
- oznacz wierzchołki krzyża greckiego literami kolejno: AB-C-DE-F-GH-I-JK-L, gdzie odcinki AB, DE, GH, JK są zewnętrznymi krawędziami ramion krzyża
- zaznacz środek odcinka AB – punkt M
- zaznacz środek odcinka EF – punkt N
- narysuj odcinek o końcach w punktach M i N
- połącz odcinkiem punkty C i J
- połącz odcinkiem punkty F i I.
Efekt pracy:
Po otrzymaniu rysunku należy krzyż grecki wyciąć (narożne kwadraty odrzucić) i poprzecinać wzdłuż narysowanych linii. Układanka gotowa, a satysfakcja gwarantowana.
Po zbadaniu własności figur i utworzeniu figury wg wzorca uczeń może wkleić efekt swojej pracy do zeszytu.
Innym sposobem na stworzenie układanki Sam Loyda jest wykorzystanie wiedzy z geometrii analitycznej. Tym razem punktem wyjścia do tworzenia poszczególnych elementów układanki będzie pięciokąt. Prosimy uczniów o zaznaczenie w układzie współrzędnych następujących figur:
- trójkąt o wierzchołkach A=(0,0), B=(5,0), C=(4,2)
- trójkąt o wierzchołkach C, D=(2,1), E=(2,2)
- trapez prostokątny o wierzchołkach A, D, E, F=(0,2)
- kwadrat o wierzchołkach E, F, G=(0,4), H=(2,4)
- sześciokąt o wierzchołkach C, E, H, G, I=(0,5), J=(2,6)
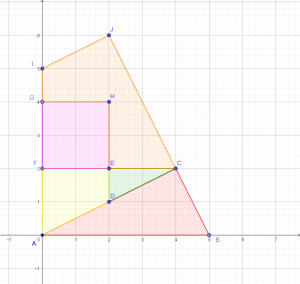
Efekt pracy przedstawia rysunek:
W ramach lekcji powtórzeniowej można badać własności figur korzystając z narzędzi geometrii analitycznej np. wykazać, że trójkąt ABC jest prostokątny, wyznaczyć kąt ostry trapezu badając kąt pomiędzy prostą AC i osią OY.
Po zbadaniu własności, pięciokąt należy wyciąć i poprzecinać na części wzdłuż zaznaczonych linii.
Kolejną propozycją do wykorzystania na lekcji jest samodzielne tworzenie układanki w GeoGebrze. Więcej… już wkrótce.